깊이우선탐색(DFS)
깊이 우선 탐색은 그래프 완전 탐색 기법 중 하나로 그래프의 시작 노드에서 출발하여 탐색할 한쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 방식이다.
구현은 재귀함수와 스택 자료구조를 사용하여 구현하고 재귀 함수를 사용하기 때문에 오버플로에 주의해야한다.
시간복잡도: O(V+E) V: 노드 수 E: 에지 수
문제유형: 단절점 찾기,단절선 찾기, 사이클 찾기, 위상정렬
인접리스트(그래프)+방문여부 체크배열
핵심이론
1.DFS를 시작한 노드를 정한 후 사용할 자료구조 초기화
2.스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입
3.스택 자료구조에 값이 없을 때까지 반복
문제 예시
연결요소의 개수 구하기
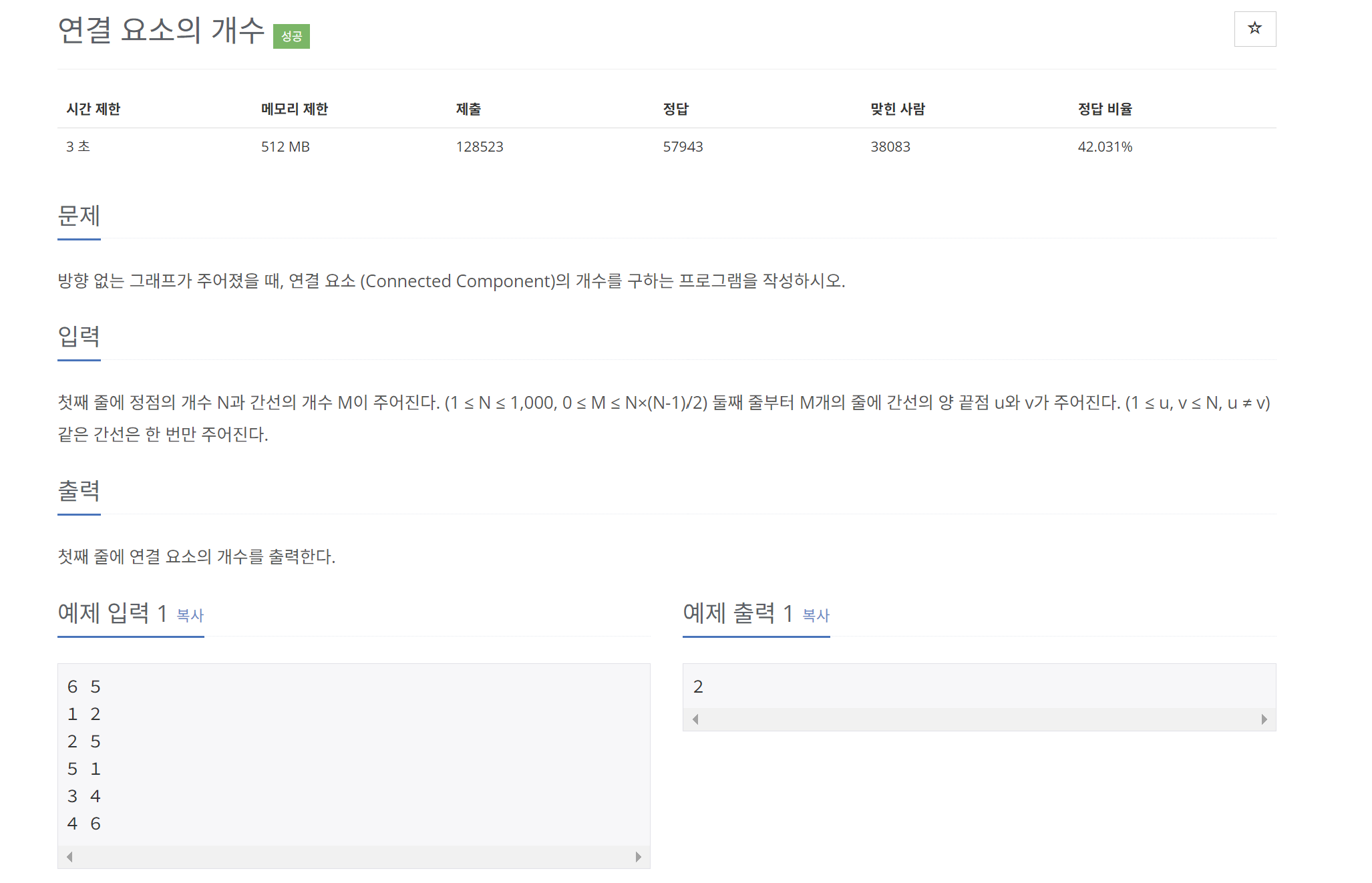
노드의 최대 개수가 1,000이여서 N^2 이하의 알고리즘을 사용해야한다.
한 번의 DFS가 끝날 때까지 탐색한 모든 노드의 집합을 하나의 연결요소로 판단할 수 있다.
#include <iostream>
#include <vector>
using namespace std;
static vector<vector<int>> a; //인접리스트
static vector<bool> visited; //방문리스트
void DFS(int v);
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n>>m;
a.resize(n + 1);
visited = vector<bool>(n + 1, false);
for (int i = 0; i < m; i++) { //인접리스트만들기
int s, e;
cin >> s >> e;
a[s].push_back(e);
a[e].push_back(s);
}
int count = 0;
for (int i = 1; i < n+1; i++) {
if (!visited[i]) { //방문하지않았다면
count++;
DFS(i);
}
}
cout << count << "\n";
}
void DFS(int v) {
if (visited[v]) return;
visited[v] = true;
for (int i : a[v]) {
if (!visited[i]) DFS(i);
}
}
너비 우선 탐색(BFS)
너비 우선 탐색은 시작노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 방식이다.
보통 Queue 자료구조를 이용하여 구현한다.
핵심이론
1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화
2.큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입
3.큐 자료구조에 값이 없을 때까지 반복
문제예시
DFS와 BFS 프로그램
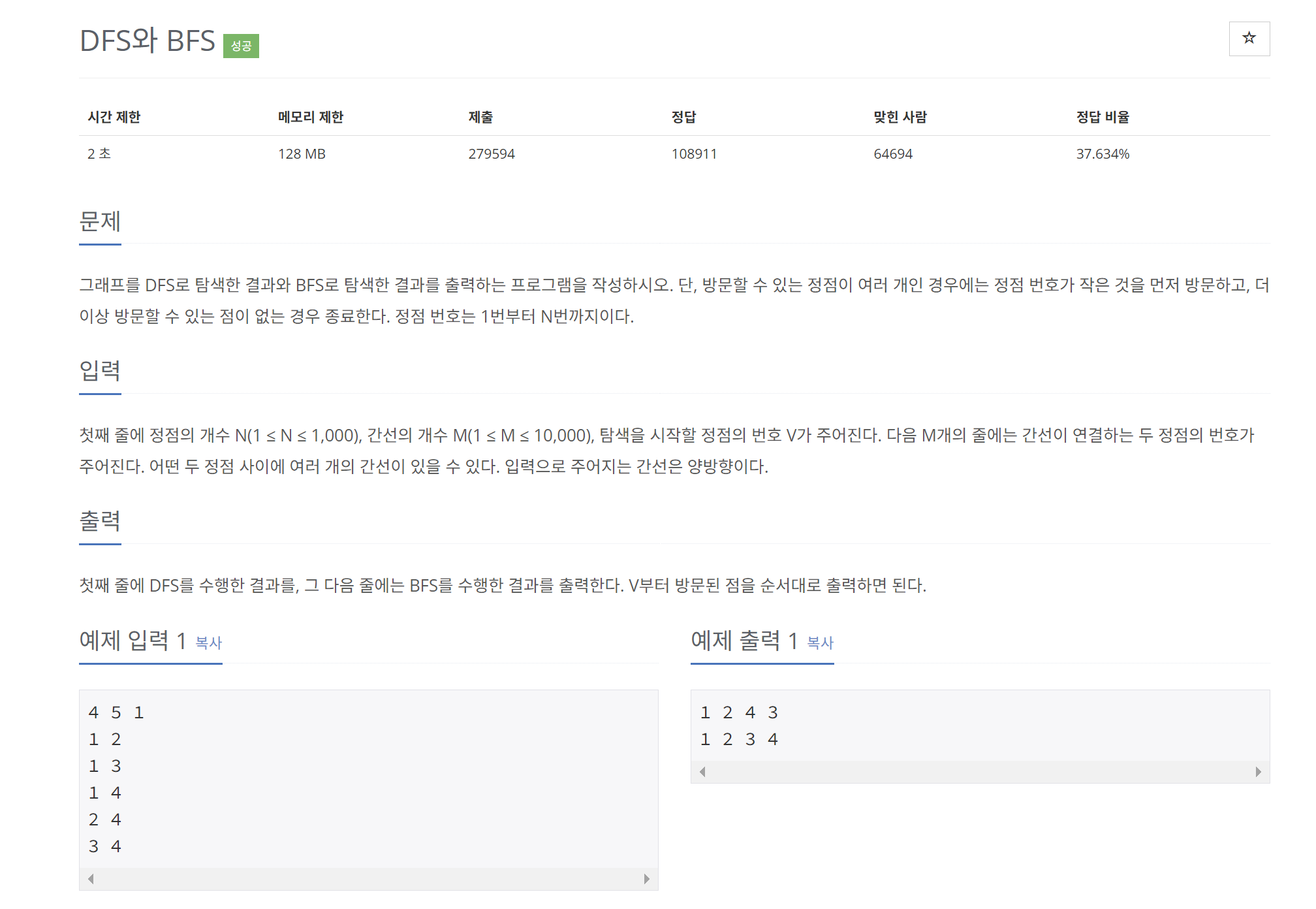
각각 DFS와 BFS를 수행한다. 수행 시에 노드를 출력해준다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
static vector<vector<int>> a; //인접리스트
static vector<bool> visited; //방문리스트
void DFS(int node);
void BFS(int node);
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m,start;
cin >> n >> m>>start;
a.resize(n + 1);
for (int i = 0; i < m; i++) { //인접리스트만들기
int s, e;
cin >> s >> e;
a[s].push_back(e);
a[e].push_back(s);
}
for (int i = 1; i <=n; i++) {
sort(a[i].begin(), a[i].end());
}
visited = vector<bool>(n + 1, false);
DFS(start);
cout << "\n";
fill(visited.begin(), visited.end(),false); //초기화
BFS(start);
cout << "\n";
}
void DFS(int node) {
cout << node << " ";
visited[node] = true;
for (int i : a[node]) {
if (!visited[i]) DFS(i);
}
}
void BFS(int node) {
queue<int> myqueue;
myqueue.push(node);
visited[node] = true;
while (!myqueue.empty()) {
int cur_node = myqueue.front();
myqueue.pop();
cout << cur_node << " ";
for (int i : a[cur_node]) {
if (!visited[i]) {
visited[i] = true;
myqueue.push(i);
}
}
}
}
미로 탐색하기
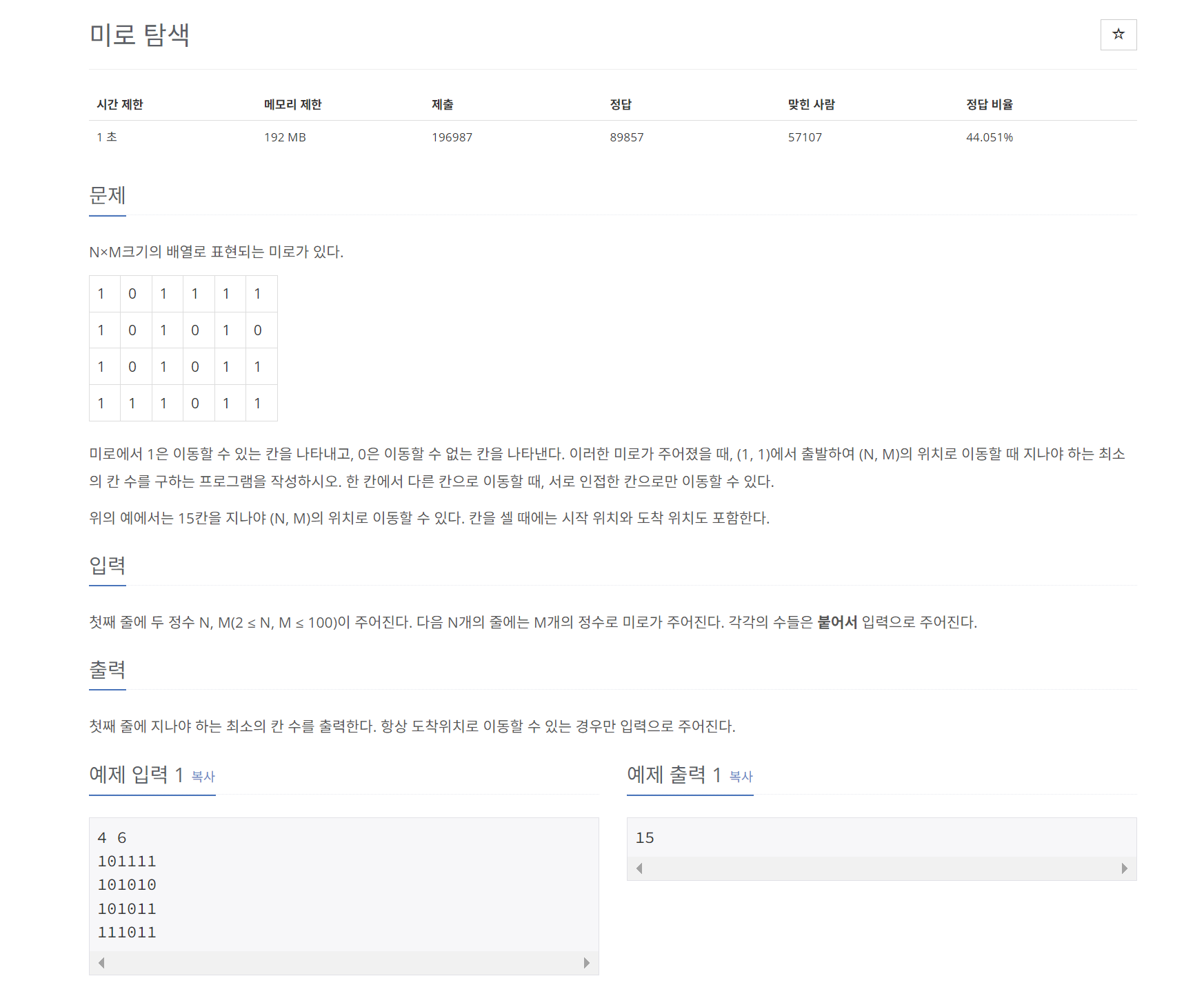
문제의 요구 사항은 지나가야하는 칸 수의 최솟값을 찾는 것, 이 값은 BFS를 사용해 최소로 도달했을 때 깊이를 출력하면 최솟값을 찾을 수 있다
이때, DFS보다 BFS가 적합한데 이유는 BFS는 해당 깊이에서 갈 수 있는 노드의 탐색을 마친 후 다음 깊이로 넘어가기 때문에 갈 수 있는 길을 모두가고 다음 길을 가기 때문에 미로에서 최솟값을 찾는데 더 효과적이다.
#include <iostream>
#include <queue>
using namespace std;
static int dx[] = { 0,1,0,-1 }; //왼 아래 오 위
static int dy[] = { -1,0,1,0 };
static int a[101][101];
static bool visited[101][101] = { false };
static int n, m;
void BFS(int i,int j);
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++) { //미로만들기
string s;
cin >> s;
for (int j = 0; j < m; j++) {
a[i][j] = s[j] - '0';
}
}
BFS(0, 0);
cout << a[n - 1][m - 1] << "\n";
}
void BFS(int i,int j) {
queue<pair<int,int>> myqueue;
myqueue.push({ i,j });
while (!myqueue.empty()) {
int now[2];
now[0] = myqueue.front().first;
now[1] = myqueue.front().second;
myqueue.pop();
visited[i][j] = true;
for (int k = 0; k < 4; k++) {
int x = now[0] + dx[k];
int y = now[1] + dy[k];
if (x >= 0 && x < n && y >= 0 && y < m) {
if (a[x][y] != 0 && !visited[x][y]) {
visited[x][y] = true;
a[x][y] = a[now[0]][now[1]] + 1;
myqueue.push({ x,y });
}
}
}
}
}'코딩테스트 > 이론' 카테고리의 다른 글
| [프로그래머스][LV 2][C++]메뉴 리뉴얼 (0) | 2024.05.27 |
|---|---|
| [코딩테스트][C++]이론6. 그리디 알고리즘 (0) | 2024.04.04 |
| [코딩테스트][C++]이론4-2. 정렬 (2) | 2024.03.16 |
| [코딩테스트][C++]이론4-1. 정렬 (0) | 2024.03.15 |
| [코딩테스트][C++]이론3. 스택과 큐 (0) | 2024.03.14 |