https://school.programmers.co.kr/learn/courses/30/lessons/12902
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

문제를 봤을 때 DP로 풀면 좋을 것 같다고 생각을 했다. 그러려면 일반 점화식을 도출해내야한다.
문제를 생각해보면 짝수에서만 가능하다는 것을 알 수 있다. 그리고 일반적인 경우를 생각해보자면
- 인 경우:
- 타일을 채울 수 없는 경우로, 한 가지 방법이 존재-> 아무것도 하지 않는 방법.
- 인 경우:
- 가로로 타일 3개 배치
- 세로로 2개를 위로 쌓아 배치
- 세로로 2개를 아래로 쌓아 배치
- 인 경우:
- 크기의 바닥을 두 번 채우는 경우와 유사하게 생각할 수 있다.
이제 점화식을 도출해보자
크기의 바닥을 채우는 방법을 찾기 위해 혹은 그 이하의 크기에서 타일을 어떻게 배치하는지 생각해보자
n의 경우의 수를 구하려면 일단 n-2번째와 n-4.. 0이 될때까지의 경우의 수를 모두 더 해주어야한다. 이때 n-4의 패턴부터는 좌우 대칭적으로 배치할 수 있기 때문에 곱하기2를 해준다.
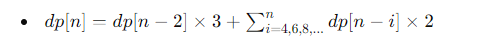
코드로 구현하면 다음과 같다
#include <string>
#include <vector>
#define MOD 1000000007
using namespace std;
//dp활용
//짝수일때만 계산가능
int solution(int n) {
if (n % 2 != 0) return 0; // 홀수일 경우 0 반환
vector<long long> dp(n + 1, 0);
dp[0] = 1; // base case
dp[2] = 3; // 기본적인 2x3 타일 배치 방법의 수
for (int i = 4; i <= n; i += 2) {
dp[i] = dp[i - 2] * dp[2];
for (int j = i - 4; j >= 0; j -= 2) {
dp[i] += dp[j] * 2;
}
dp[i] %= MOD;
}
return dp[n];
}
'코딩테스트 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스][C++][LV2]당구 연습 (1) | 2024.08.13 |
|---|---|
| [프로그래머스][LV2][C++]교점에 별 만들기 (1) | 2024.07.16 |
| [프로그래머스][LV2][C++][PCCP 기출문제] 2번 / 석유 시추 (0) | 2024.07.12 |
| [프로그래머스][LV2][C++]택배 배달과 수거하기 (0) | 2024.07.11 |
| [프로그래머스][LV2][C++]순위검색 (0) | 2024.07.10 |
