코딩테스트 공부를 하다가 난이도가 올라갈 수록 알고리즘을 분석하고 여러유형에 대해 이론적으로 이해하고 있는 부분이 부족하다고 생각이 들어 알고리즘과 여러 유형에 대해 익혀보는 시간을 가져보려고 한다.
1. 구간 합
구한 합의 핵심이론은 a~b 구간 사이의 합을 구하는 것이다. 이 때, 배열을 두고 직접 합을 구할 때, 최악의 경우 i가 0이고 j가 N인 경우 시간복잡도가 O(N)이 나와서 연산 수가 많아지면 시간초과가 뜰 수 있다. 구간 합의 경우 연산 수 가 많아지는 경우가 많기 때문에 배열 합을 쓰는게 좋다.
*합 배열
합 배열은 기존의 배열에서 구간마다의 합을 만들어두는 것으로 이 배열을 만들어 두고 이를 활용하여 정답을 구한다면
연산수가 O(1)로 줄어들게 된다.
-1차원에서의 합 배열
1차원 배열에서 합 배열을 만들 때 S가 합배열이고 B가 배열이라고 했을 때, S[i]=S[i-1] + B[i] 이다.
그리고 만약 i~j까지의 구간 합을 구한다면 S[j] -S[i] 로 정답을 구할 수 있다.
-2차원에서의 합 배열
2차원 배열에서 합 배열을 만들 때는 경우의 수를 2가지 생각해주어야 한다
일단 1행일때 열이 변하는경우, 1열일때, 행이 변하는 경우를 생각해보자면 1차원에서의 합 배열을 구하는 공식과 똑같은데
1행 일때 -> S[i][j] = S[1][j-1]+B[i][j]
1열 일때 -> S[i][j] = S[i-1][i]+ B[i][j]
-> 전까지의 합 + 현재위치의 값
나머지 행과 열 일때
S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+B[i][j]
-> i-1 값(이전 값의 행)에서 열 방향에서의 합 + j-1(이전 값의 열)값에서 행 방향 + 중복되게 더해진 값 - 현재 위치의 값
그리고 X1,Y1 ~ X2,Y2 까지의 구간 합을 구한다면
S[X2][Y2]-S[X1-1][Y2]-S[X2][Y1-1]+S[X1][Y1]
->X2,Y2까지의 구간합 - X1-1 값에서의 열 방향에서의 합 - Y1-1 값에서의 행 방향에서의 합 + 중복되게 빼진 값
예시 문제
나머지 합 구하기
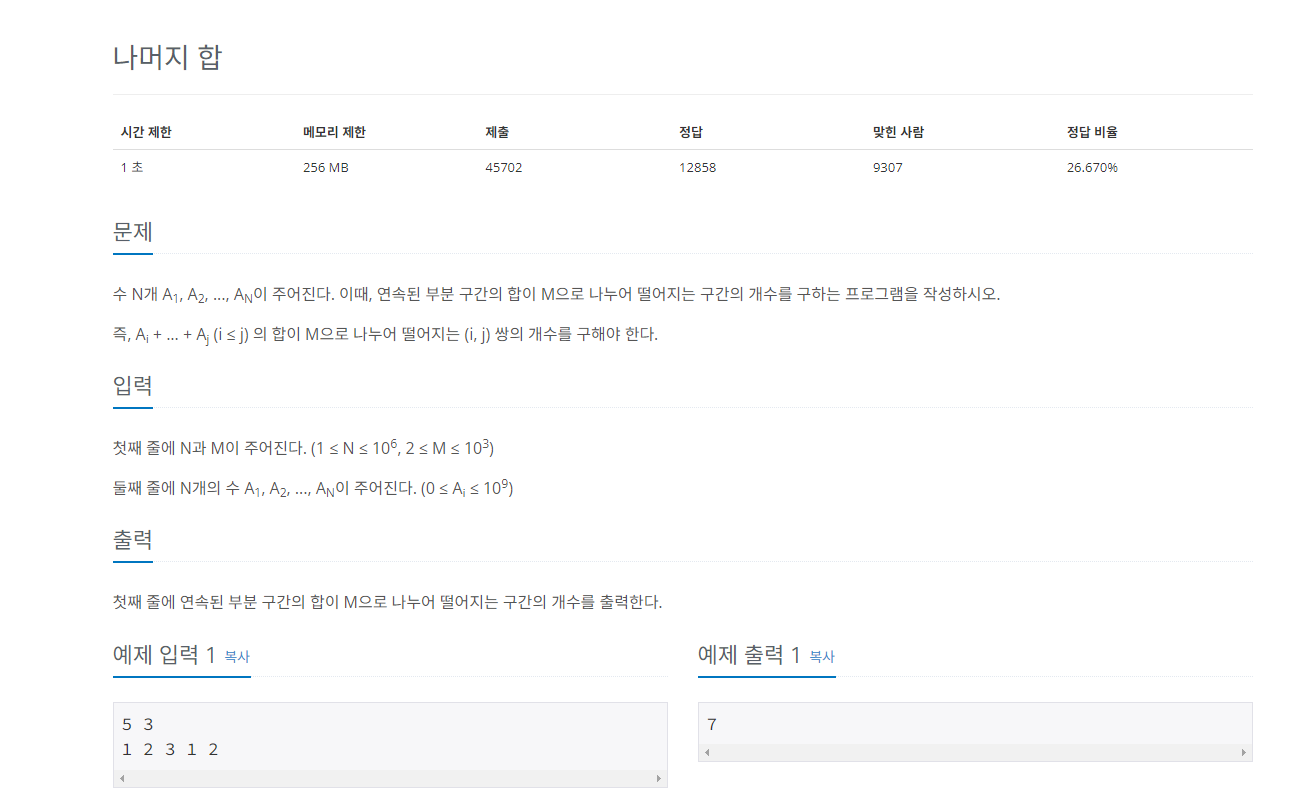
이 문제에서 보면 N의 최대값이 10^6으로 최악의 경우 1초안에 연산하기는 힘들기 때문에 합 배열을 사용해야한다.
※핵심 아이디어
1. (A+B) % C = ((A%C)+(B%C))%C -> 특정 구간 수를 나머지 연산해서 더한 값을 나머지 연산하는 것이나 구간합을 나머지 연산한 값이나 같다.
2. if S[j]%M == S[i]%M 이라면 (S[j]-S[i])%M==0이다.
흐름을 살펴보자면
1. 합 배열을 만든다.
2. %M의 값으로 배열을 업데이트 해준다.
3. 경우의 수를 세어준다. (0일때는 0인 개수만큼 경우의 수를 추가, 2보다 클때에는 조합을 통해 경우의 수를 추가)
#include <iostream>
#include <vector>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
cin >> N >> M;
vector<long> S(N, 0);
vector<long> C(N, 0);
long answer = 0;
cin >> S[0];
for (int i = 1; i < N; i++) {
int tmp = 0;
cin >> tmp;
S[i] = S[i - 1] + tmp;
}
for (int i = 0; i < N; i++) {
int r = S[i] % M;
if (r == 0) {
answer++;
}
C[r]++;
}
for (int i = 0; i < M; i++) {
if (C[i] > 1) {
answer += (C[i] * (C[i] - 1) / 2);
}
}
cout << answer << "\n";
}
'코딩테스트 > 이론' 카테고리의 다른 글
| [코딩테스트][C++]이론5. DFS 와 BFS (0) | 2024.03.29 |
|---|---|
| [코딩테스트][C++]이론4-2. 정렬 (2) | 2024.03.16 |
| [코딩테스트][C++]이론4-1. 정렬 (0) | 2024.03.15 |
| [코딩테스트][C++]이론3. 스택과 큐 (0) | 2024.03.14 |
| [코딩테스트][C++]이론2. 투 포인터 (2) | 2024.03.13 |