강의
학습 페이지
www.inflearn.com
1.Intersection
물체들끼리의 충돌했을 때 상호작용을 해주기 위해서는 우선 충돌을 탐지해야한다. 탐지하는 것을 Intersection이라고 한다.
구와 구
만약 교점이 있는지 확인하려면 각 원의 원점간의 거리를 계산했을 그 크기가 각 반지름의 합과 같거나 작다면 붙어있거나
구가 충돌이 있거나 겹쳐져있는 것이다. 이때 계산의
bool MathUtils::SphereSphere(const Sphere3D& s1, const Sphere3D& s2)
{
float sum = s1.radius + s2.radius;
//제곱으로 비교
float sqDistance = (s1.position - s2.position).LengthSquared();
return sqDistance <= sum * sum;
}
구와 AABB
구와 AABB는 원과 원을 비교할 때와 비슷한 느낌으로 원과 AABB의 최근접점까지의 거리와 반지름을 비교해서 최근접점까지의 거리가 더 짧으면 충돌이 있다는 것을 알 수 있다.
bool MathUtils::SphereAABB(const Sphere3D& sphere, const AABB3D& aabb)
{
Point3D closestPoint = ClossetPoint(aabb, sphere.position);
float distSq = (sphere.position - closestPoint).LengthSquared();
float radiusSq = sphere.radius * sphere.radius;
return distsq < radiusSq;
}
구와 OBB
구와 obb는 AABB와 같이 최근접점과의 거리와 반지름을 비교해주면 된다.
bool MathUtils::SphereOBB(const Sphere3D& sphere, const OBB3D& obb)
{
Point3D closestPoint = ClossetPoint(obb, sphere.position);
float distSq = (sphere.position - closestPoint).LengthSquared();
float radiusSq = sphere.radius * sphere.radius;
return distsq < radiusSq;
}
구와Plane
구와 Plane도 동일하게 최근접점과의거리와 반지름을 비교해주면 된다.
// 구와 평면의 충돌 검사
bool MathUtils::SphereToPlane(const Sphere3D& sphere, const Plane3D& plane)
{
Point3D closestPoint = ClosestPoint(plane, sphere.position);
float distSq = (sphere.position - closestPoint).LengthSquared();
float radiusSq = sphere.radius * sphere.radius;
return distSq < radiusSq;
}AABB와 AABB
각 큐브의 min max를 통해 비교해준다. 사이에 있는 값이 있는지 검사해준다.
// AABB와 AABB의 충돌 검사
bool MathUtils::AABBToAABB(const AABB3D& aabb1, const AABB3D& aabb2)
{
Point3D aMin = AABB3D::GetMin(aabb1); // aabb1의 최소 좌표
Point3D aMax = AABB3D::GetMax(aabb1); // aabb1의 최대 좌표
Point3D bMin = AABB3D::GetMin(aabb2); // aabb2의 최소 좌표
Point3D bMax = AABB3D::GetMax(aabb2); // aabb2의 최대 좌표
return (aMin.x <= bMax.x && aMax.x >= bMin.x) &&
(aMin.y <= bMax.y && aMax.y >= bMin.y) &&
(aMin.z <= bMax.z && aMax.z >= bMin.z); // 모든 축에 대해 겹치면 true
}AABB와 OBB
각 선분에 대해 기준이 되는 축을 하나 정하고 프로젝션(SAT알고리)을 모든 선분에 해줬을 때 선분이 모든 축에서 겹치는 부분이 있다면 충돌이 있는 것이다. 이때 정확한 판별을 위하여 외적한 축을 바탕으로도 이 연산을 해주어야 한다.
// AABB의 주어진 축에 대한 구간을 계산
Interval3D MathUtils::GetInterval(const AABB3D& aabb, const Vec3& axis)
{
Vec3 i = AABB3D::GetMin(aabb); // 최소 좌표
Vec3 a = AABB3D::GetMax(aabb); // 최대 좌표
Vec3 vertex[8] =
{
Vec3(i.x, a.y, a.z), Vec3(i.x, a.y, i.z), Vec3(i.x, i.y, a.z), Vec3(i.x, i.y, i.z),
Vec3(a.x, a.y, a.z), Vec3(a.x, a.y, i.z), Vec3(a.x, i.y, a.z), Vec3(a.x, i.y, i.z),
};
Interval3D result; // 구간 초기화
result.min = result.max = axis.Dot(vertex[0]); // 첫 정점을 기준으로 초기화
for (int i = 1; i < 8; ++i)
{
float projection = axis.Dot(vertex[i]);
result.min = min(result.min, projection); // 최소값 갱신
result.max = max(result.max, projection); // 최대값 갱신
}
return result; // 계산된 구간 반환
}
// OBB와 주어진 축에 대한 구간(Interval) 계산
Interval3D MathUtils::GetInterval(const OBB3D& obb, const Vec3& axis)
{
Vec3 vertex[8]; // OBB의 꼭짓점을 저장할 배열
Vec3 C = obb.position; // OBB의 중심 위치
Vec3 E = obb.size; // OBB의 크기(각 축에 대한 반 길이)
vector<Vec3> A; // OBB의 축
A.push_back(obb.orientation.Right()); // OBB의 오른쪽 방향 축
A.push_back(obb.orientation.Up()); // OBB의 위쪽 방향 축
A.push_back(obb.orientation.Backward()); // OBB의 뒤쪽 방향 축
// OBB의 8개 꼭짓점 계산
vertex[0] = C + A[0] * E.x + A[1] * E.y + A[2] * E.z;
vertex[1] = C - A[0] * E.x + A[1] * E.y + A[2] * E.z;
vertex[2] = C + A[0] * E.x - A[1] * E.y + A[2] * E.z;
vertex[3] = C + A[0] * E.x + A[1] * E.y - A[2] * E.z;
vertex[4] = C - A[0] * E.x - A[1] * E.y - A[2] * E.z;
vertex[5] = C + A[0] * E.x - A[1] * E.y - A[2] * E.z;
vertex[6] = C - A[0] * E.x + A[1] * E.y - A[2] * E.z;
vertex[7] = C - A[0] * E.x - A[1] * E.y + A[2] * E.z;
// 주어진 축에 대해 OBB의 꼭짓점들을 투영하여 최소/최대 값 계산
Interval3D result;
result.min = result.max = axis.Dot(vertex[0]); // 첫 꼭짓점으로 초기화
for (int i = 1; i < 8; ++i)
{
float projection = axis.Dot(vertex[i]); // 꼭짓점을 축에 투영
result.min = min(result.min, projection); // 최소값 갱신
result.max = max(result.max, projection); // 최대값 갱신
}
return result; // 계산된 구간 반환
}
// AABB와 OBB가 주어진 축에 대해 겹치는지 검사
bool MathUtils::OverlapOnAxis(const AABB3D& aabb, const OBB3D& obb, const Vec3& axis)
{
Interval3D a = GetInterval(aabb, axis); // AABB의 구간 계산
Interval3D b = GetInterval(obb, axis); // OBB의 구간 계산
return ((b.min <= a.max) && (a.min <= b.max)); // 구간이 겹치면 true 반환
}
// AABB와 OBB의 충돌 검사
bool MathUtils::AABBToOBB(const AABB3D& aabb, const OBB3D& obb)
{
Vec3 test[15] = // 충돌 검사에 사용될 축
{
Vec3(1,0,0), // AABB 축 1
Vec3(0,1,0), // AABB 축 2
Vec3(0,0,1), // AABB 축 3
obb.orientation.Right(), // OBB 축 1
obb.orientation.Up(), // OBB 축 2
obb.orientation.Backward(), // OBB 축 3
// 외적으로 생성된 추가 축
};
// 추가 축 계산 (AABB 축과 OBB 축의 외적)
for (int i = 0; i < 3; ++i)
{
test[6 + i * 3 + 0] = test[i].Cross(test[3]);
test[6 + i * 3 + 1] = test[i].Cross(test[4]);
test[6 + i * 3 + 2] = test[i].Cross(test[5]);
}
// 모든 축에 대해 겹치는지 검사
for (int i = 0; i < 15; ++i)
{
if (!OverlapOnAxis(aabb, obb, test[i])) // 하나라도 겹치지 않으면 false 반환
return false;
}
return true; // 모두 겹치면 true 반환
}
AABB와 PLANE
평명은 쭉 뻗어나가는 것으로 거리 계산을 통해 해주면 된다.
// AABB와 평면의 충돌 검사
bool MathUtils::AABBToPlane(const AABB3D& aabb, const Plane3D& plane)
{
float pLen = aabb.size.x * fabsf(plane.normal.x) +
aabb.size.y * fabsf(plane.normal.y) +
aabb.size.z * fabsf(plane.normal.z);
float dot = plane.normal.Dot(aabb.position); // 평면의 법선과 AABB 중심의 내적
float dist = dot - plane.distance; // 평면 상수와의 차이 계산
return fabsf(dist) <= pLen; // 겹치는지 여부 반환
}
OBB와 OBB
이것도 동일하게 축을 하나 정하고 이를 모든 선분을 검사해주면 된다.
// 두 OBB가 주어진 축에 대해 겹치는지 검사
bool MathUtils::OverlapOnAxis(const OBB3D& obb1, const OBB3D& obb2, const Vec3& axis)
{
Interval3D a = GetInterval(obb1, axis); // obb1의 구간 계산
Interval3D b = GetInterval(obb2, axis); // obb2의 구간 계산
return ((b.min <= a.max) && (a.min <= b.max)); // 구간이 겹치면 true 반환
}
// 두 OBB의 충돌 검사
bool MathUtils::OBBToOBB(const OBB3D& obb1, const OBB3D& obb2)
{
Vec3 test[15] = // 충돌 검사에 사용될 축
{
obb1.orientation.Right(), // OBB1 축 1
obb1.orientation.Up(), // OBB1 축 2
obb1.orientation.Backward(), // OBB1 축 3
obb2.orientation.Right(), // OBB2 축 1
obb2.orientation.Up(), // OBB2 축 2
obb2.orientation.Backward(), // OBB2 축 3
// 외적으로 생성된 추가 축은 여기에서 계산됨
};
// 추가 축 계산 (OBB1 축과 OBB2 축의 외적)
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j) {
test[6 + i * 3 + j] = test[i].Cross(test[3 + j]);
}
}
// 모든 축에 대해 겹치는지 검사
for (int i = 0; i < 15; ++i)
{
if (!OverlapOnAxis(obb1, obb2, test[i])) // 하나라도 겹치지 않으면 false 반환
return false;
}
return true; // 모두 겹치면 true 반환
}
Plane과 Plane
각 평면의 법선벡터를 외적해서 평행한지 검사하고 평행하지 않으면 충돌이 있는것이다.
// 두 평면의 충돌 검사
bool MathUtils::PlaneToPlane(const Plane3D& plane1, const Plane3D& plane2)
{
Vec3 d = plane1.normal.Cross(plane2.normal); // 두 평면의 법선 벡터의 외적
return d.Dot(d) != 0; // 외적의 결과가 0이 아니면 두 평면은 평행하지 않은 것으로 간주
}
2.RayCasting
Sphere
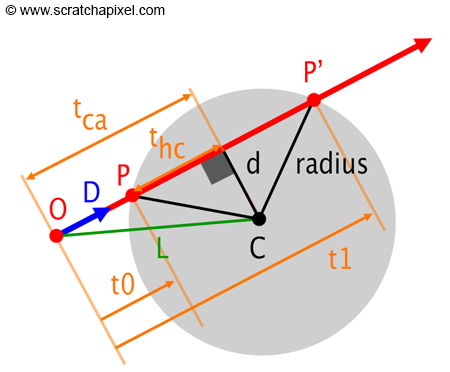
Sphere와 레이의 충돌여부 판정은 레이의 시작점과 구의 중심점까지의 거리와 반지름을 비교해서 판정한다.
// 구와 레이의 충돌 검사
bool MathUtils::Raycast(const Sphere3D& sphere, const Ray3D& ray, OUT float& distance)
{
Vec3 e = sphere.position - ray.origin; // 레이의 시작점에서 구의 중심까지의 벡터
float rSq = sphere.radius * sphere.radius;
float eSq = e.LengthSquared(); // e 벡터의 길이의 제곱
float a = e.Dot(ray.direction); // 레이 방향과 e 벡터의 내적
//피타고라스 공식
float bSq = eSq - (a * a); // b의 제곱(삼각형의 한 변의 제곱)
float f = sqrt(rSq - bSq); // f는 삼각형의 다른 변(구의 반지름에서 b를 뺀 값)
// 실제 충돌이 발생하지 않는 경우 -> 내적값으로 구한 반지름이랑 차이가 나면
if (rSq - (eSq - (a * a)) < 0.0f)
return false;
// 레이의 시작점이 구 내부에 있는 경우
if (eSq < rSq)
{
distance = a + f; // 구를 뚫고 나가는 지점까지의 거리
return true;
}
// 구 외부에서 시작하여 구에 닿지 않는 경우
distance = a - f; // 구에 가장 가까운 점까지의 거리
return false;
}
AABB
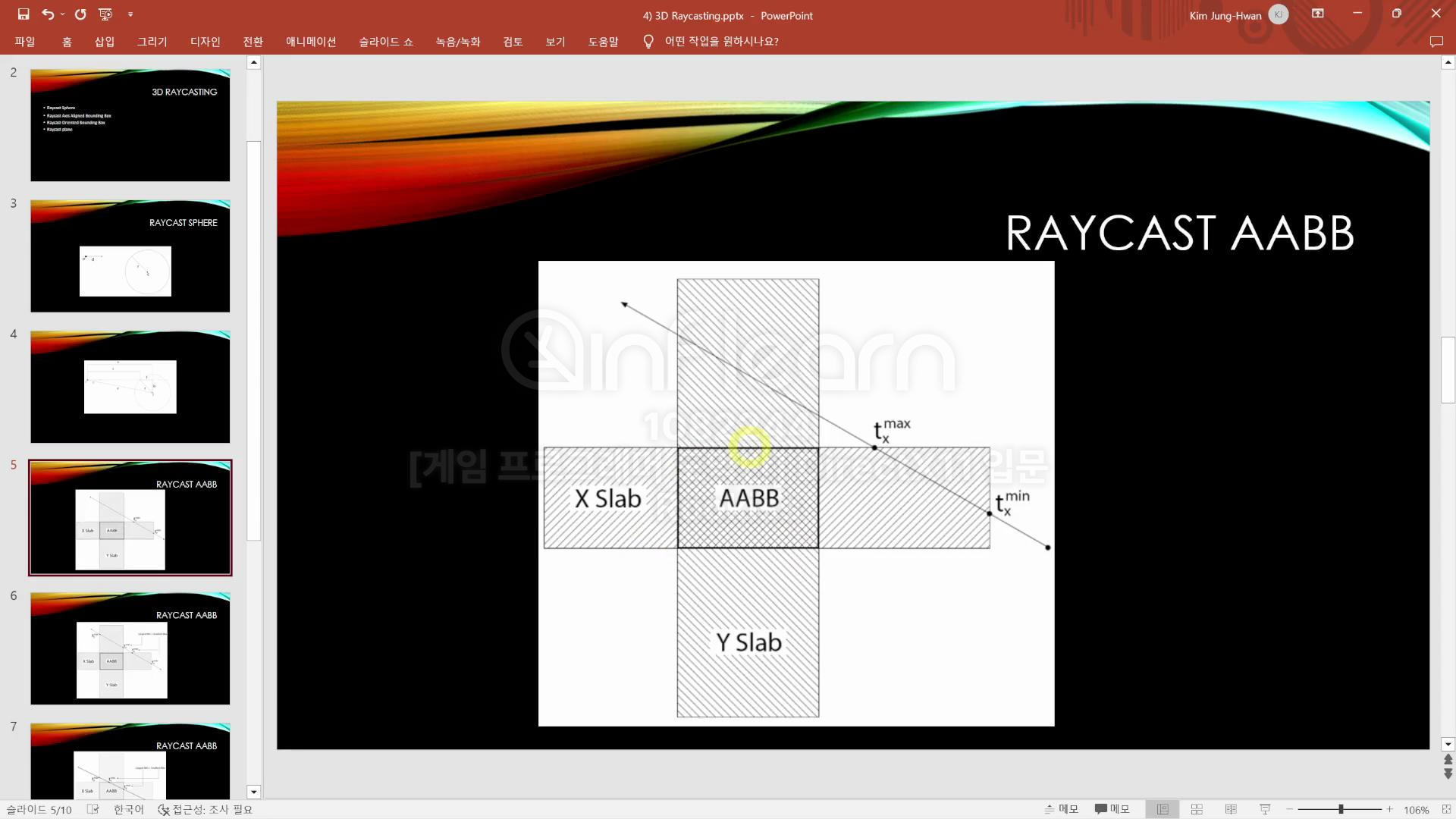
AABB와의 충돌계산은 위 사진과 같이 큐브를 위에서 봤다고 가정하고 2차원으로 생각하고 보면 평면에 대해 교차점을 찾아내면 되는데 이는 Cyrus-Beck 클리핑 알고리즘을 변형한 형태로 수행되며, tmin과 tmax를 통해 충돌이 발생하는지 판단한다.
이 테스트는 3번에 걸쳐서 해주면 된다.
// AABB와 레이의 충돌 검사 (Cyrus-Beck clipping algorithm을 사용)
bool MathUtils::Raycast(const AABB3D& aabb, const Ray3D& ray, OUT float& distance)
{
Vec3 min = AABB3D::GetMin(aabb); // AABB의 최소 좌표
Vec3 max = AABB3D::GetMax(aabb); // AABB의 최대 좌표
// 각 축에 대해 레이가 AABB의 두 평면(최소값, 최대값)과 만나는 t 값을 계산
float t1 = (min.x - ray.origin.x) / ray.direction.x;
float t2 = (max.x - ray.origin.x) / ray.direction.x;
float t3 = (min.y - ray.origin.y) / ray.direction.y;
float t4 = (max.y - ray.origin.y) / ray.direction.y;
float t5 = (min.z - ray.origin.z) / ray.direction.z;
float t6 = (max.z - ray.origin.z) / ray.direction.z;
// 가장 큰 최소 t 값(tmin)과 가장 작은 최대 t 값(tmax)을 계산
float tmin = fmaxf(fmaxf(fminf(t1, t2), fminf(t3, t4)), fminf(t5, t6));
float tmax = fminf(fminf(fmaxf(t1, t2), fmaxf(t3, t4)), fmaxf(t5, t6));
// tmax가 0보다 작으면 레이는 AABB의 뒤쪽을 향함
if (tmax < 0)
return false;
// tmin이 tmax보다 크면 레이는 AABB를 교차하지 않음
if (tmin > tmax)
return false;
// 실제 충돌 거리 계산
distance = (tmin < 0.0f) ? tmax : tmin;
return true;
}Plane
평면과의 충돌 검사는 레이가 평행한지 검사하고 아니라면 교점을 찾아내는 과정을 수행해주면 된다.
// 평면과 레이의 충돌 검사
bool MathUtils::Raycast(const Plane3D& plane, const Ray3D& ray, OUT float& distance)
{
float nd = ray.direction.Dot(plane.normal); // 레이 방향과 평면의 법선의 내적
float pn = ray.origin.Dot(plane.normal); // 레이의 시작점과 평면의 법선의 내적
// nd가 0보다 크거나 같으면 레이와 평면은 평행하거나 레이가 평면에서 멀어짐
if (nd >= 0.0f)
return false;
// 실제 충돌 거리 계산
float t = (plane.distance - pn) / nd;
if (t >= 0.0f) {
distance = t; // 충돌 지점까지의 거리
return true;
}
return false;
}
'게임공부 > Directx11' 카테고리의 다른 글
| [Directx11][C++][3D]33. 직교투영 (0) | 2024.10.10 |
|---|---|
| [Directx11][C++][3D]32. 수학3(Triangle) (4) | 2024.10.09 |
| [Directx11][C++][3D]30. 도형 (0) | 2024.10.07 |
| [Directx11][C++][3D]29. Terrain Picking (0) | 2024.10.07 |
| [Directx11][C++][3D]28. Collision(Box) & Picking (0) | 2024.10.06 |