코딩생존기

1. 퀵정렬

퀵정렬은 기준값(pivot)을 선정해 해당 값보다 작은 데이터를 왼쪽에 큰 데이터를 오른쪽에 분류하는 것을 반복해 정렬한다. 

문제 예시1.

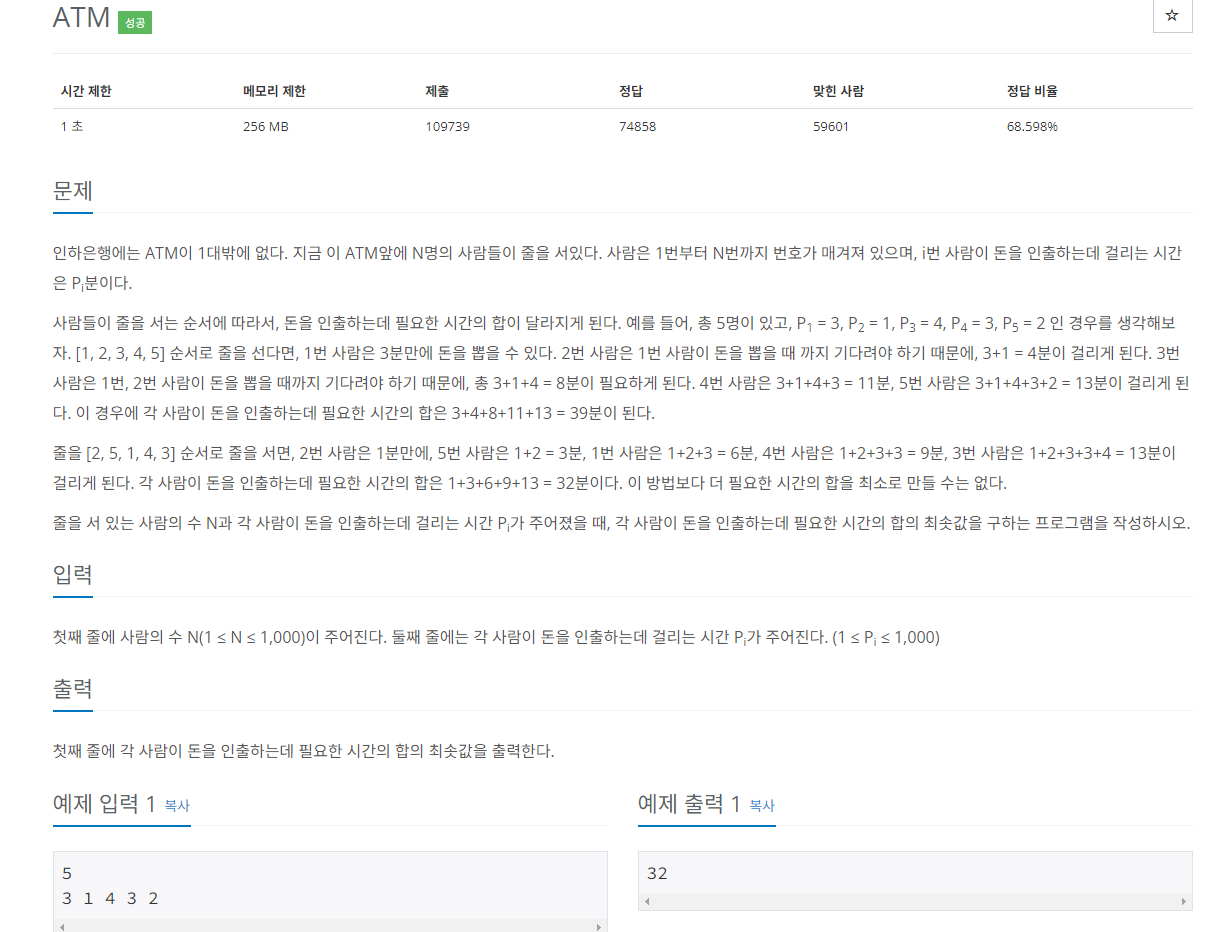
K번째 수 구하기

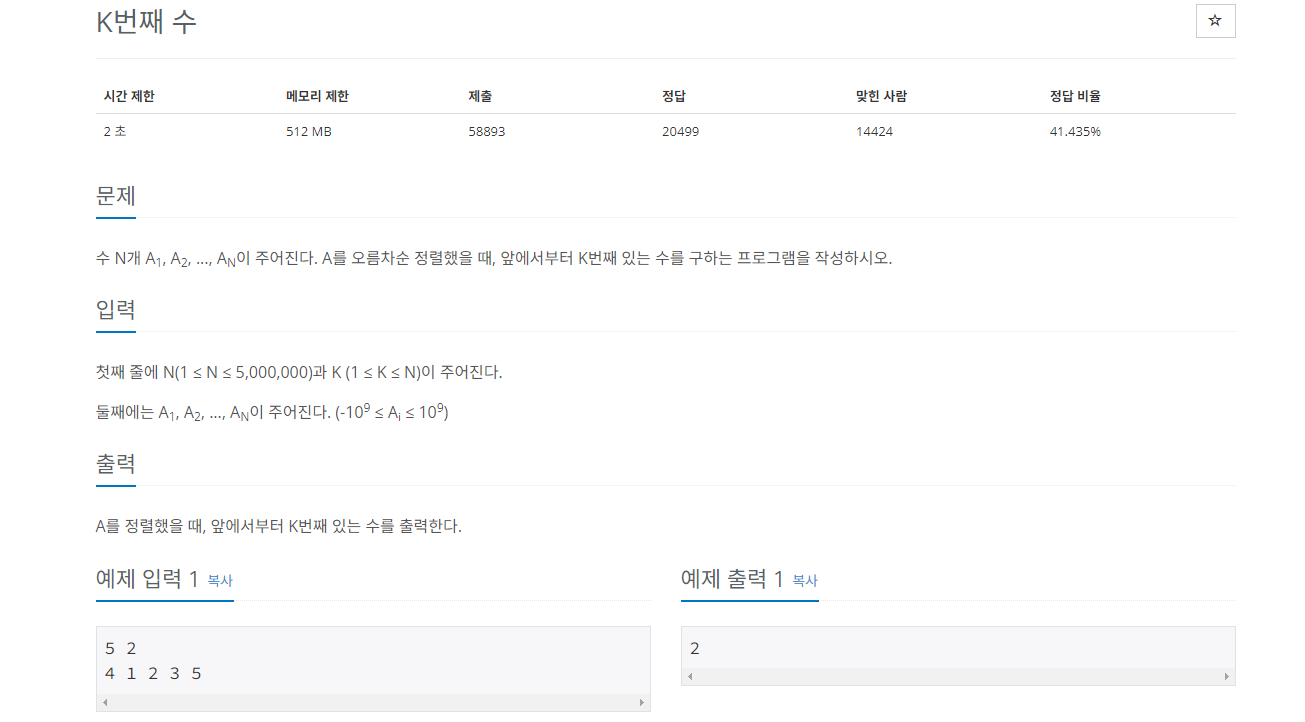
내장함수를 통해서 정렬할 수 도 있지만  퀵정렬의 원리를 이해하기위해 퀵정렬로 풀어보려고 한다.  

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void quickSort(vector<int>& A, int S, int E, int K);
int partition(vector<int>& A, int S, int E);
void swap(vector<int>& A, int i, int j);

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N, K;
    cin >> N >> K;
    vector<int> A(N, 0);
    for (int i = 0; i < N; i++) {
        cin >> A[i];
    }
    quickSort(A, 0, N - 1, K - 1);
    cout << A[K - 1];
}

void quickSort(vector<int>& A, int S, int E, int K) {
    int pivot = partition(A, S, E);
    if (pivot == K)
        return;
    else if (K < pivot) 
        quickSort(A, S, pivot - 1, K);
    else 
        quickSort(A, pivot + 1, E, K);
}
int partition(vector<int>& A, int S, int E) {
    if (S + 1 == E) {
        if (A[S] > A[E])swap(A, S, E);
        return E;
    }
    int M = (S + E) / 2;
    swap(A, S, M); 
    int pivot = A[S];
    int i = S + 1, j = E;
    while (i <= j) {
        while (j >= S + 1 && pivot < A[j]) {   
            j--;
        }
        while (i <= E && pivot > A[i]) {  
            i++;
        }

        if (i < j) {
            swap(A, i++, j--);  // 찾은 i와 j를 교환하기
        }
        else {
            break;
        }
    }
    // i == j 피벗의 값을 양쪽으로 분리한 가운데에 오도록 설정하기
    A[S] = A[j];
    A[j] = pivot;
    return j;
}
void swap(vector<int>& A, int i, int j) {
    int temp = A[i];
    A[i] = A[j];
    A[j] = temp;
}

2.병합정렬

병합 정렬은 divide and conquer 방식 즉 배열은 나누고 합치는 과정에서 정렬을 해주는 방식이다. 

문제 예시2.

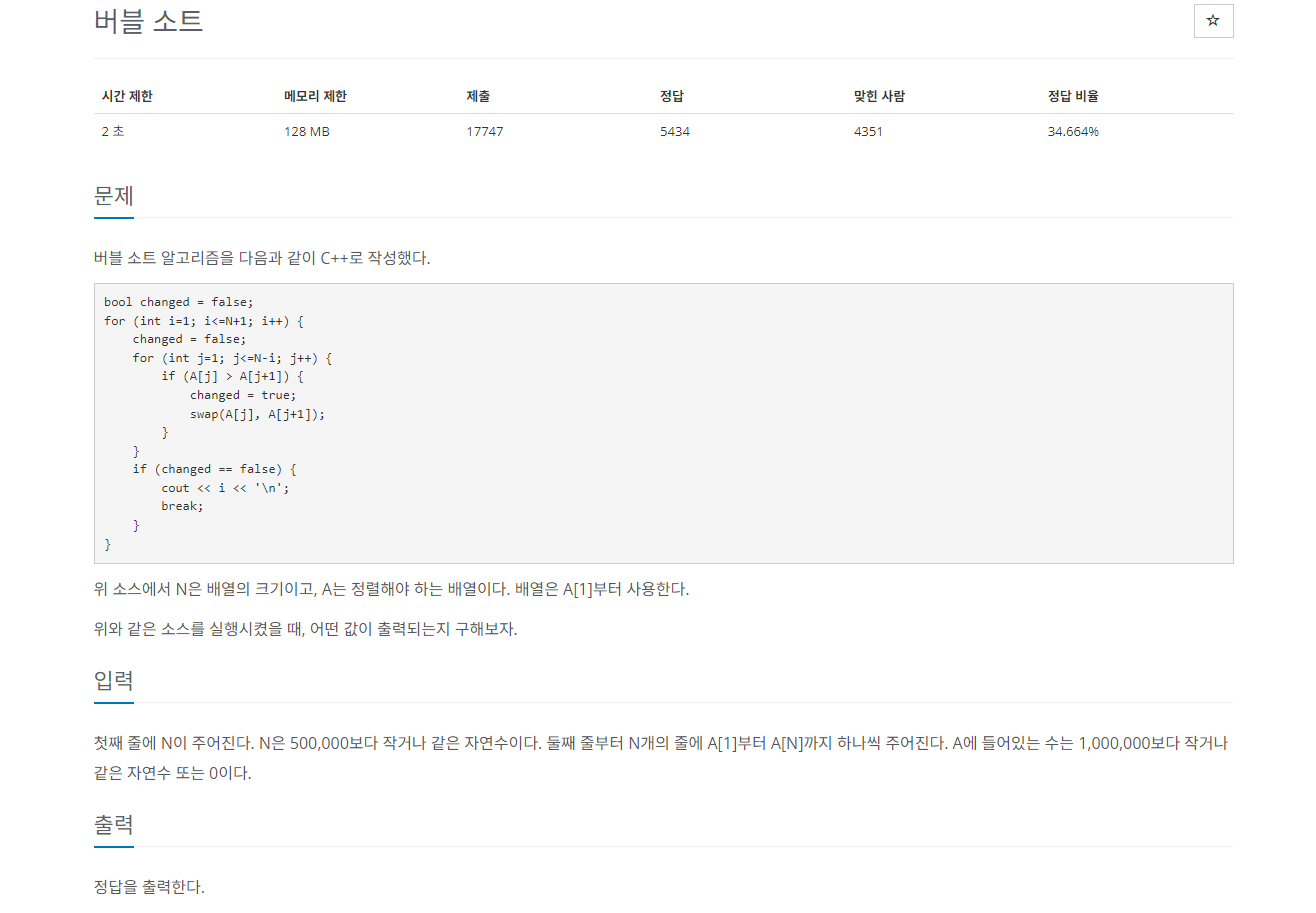
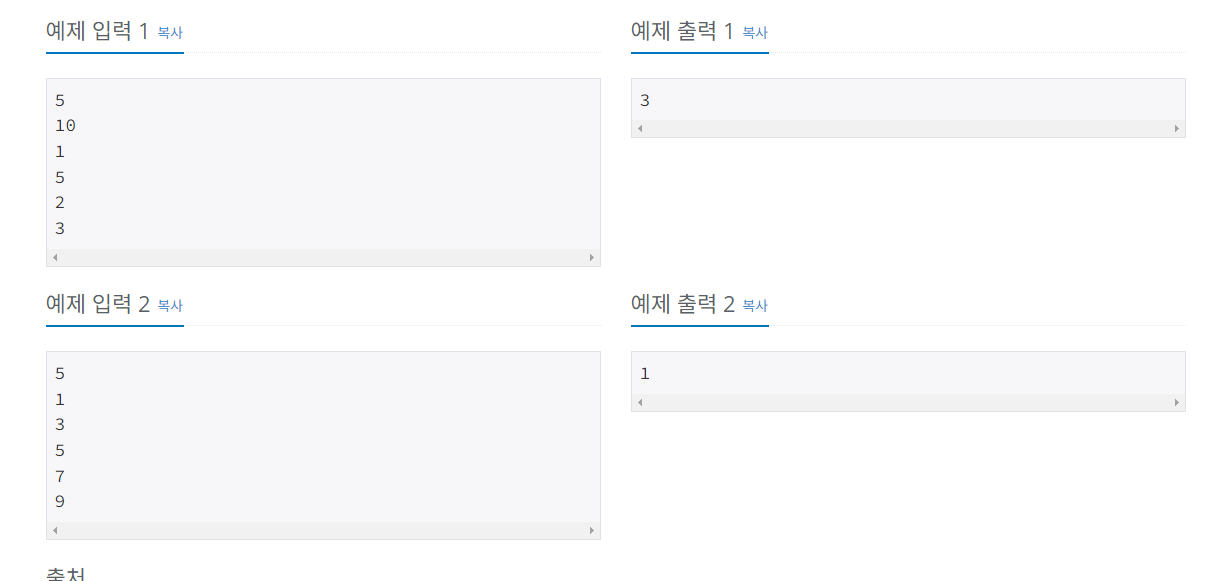
버블정렬프로그램2

n의 최대 범위가 500,000이므로 O(nlogn)의 시간복잡도로 정렬을 수행하면 된다.

하지만 제목처럼 버블정렬을 사용하면 제한 시간을 초과한다. 그런데 병합정렬의 수행과정을 보면 swap이 포함되어 있기때문에 정렬하는 과정에서 원소가 앞으로 이동한 거리만큼 더해서 그 값을 출력해주면 된다.

#include <iostream>
#include <vector>
using namespace std;
void merge_sort(int s,int e);
static vector<int> a;
static vector<int> tmp;
static long result;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int n;
    cin >> n;
    a = vector<int>(n + 1, 0);
    tmp= vector<int>(n + 1, 0);

    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    result = 0;
    merge_sort(1, n);
    cout << result << "\n";
}

void merge_sort(int s, int e) {
    if (e - s < 1) {
        return;
    }

    int m = s + (e - s) / 2;            //중앙값

    merge_sort(s, m);                   //시작~중앙
    merge_sort(m + 1, e);               //중앙~끝
    
    for (int i = s; i <= e; i++) {
        tmp[i] = a[i];
    }

    int k = s;
    int idx1 = s;
    int idx2 = m + 1;

    while (idx1 <= m && idx2 <= e) {            //병합
        if (tmp[idx1] > tmp[idx2]) {
            a[k] = tmp[idx2];               //값을 작은값으로 업데이트 해주기 
            result += idx2 - k;         //이동한 만큼 더해주기
            k++;
            idx2++;
        }
        else {
            a[k] = tmp[idx1];
            k++;
            idx1++;
        }
    }

    while (idx1 <= m) {         //남은값 배열에 채워주기
        a[k] = tmp[idx1];
        k++;
        idx1++;
    }
    while (idx2 <= e) {         //남은값 배열에 채워주기
        a[k] = tmp[idx2];
        k++;
        idx2++;
    }
}

3. 기수정렬

기수정렬은 값을 비교하는 것이아니라 값을 놓고 비교할 자릿수를 정한다음 해당 자릿수만 비교하여 정렬하는 것으로

시간복잡도는 O(kn)으로 k가 데이터의 자릿수이다.

기수 정렬은 값의 자릿수를 대표하는 10개의 큐를 사용한다. 

문제예시3.

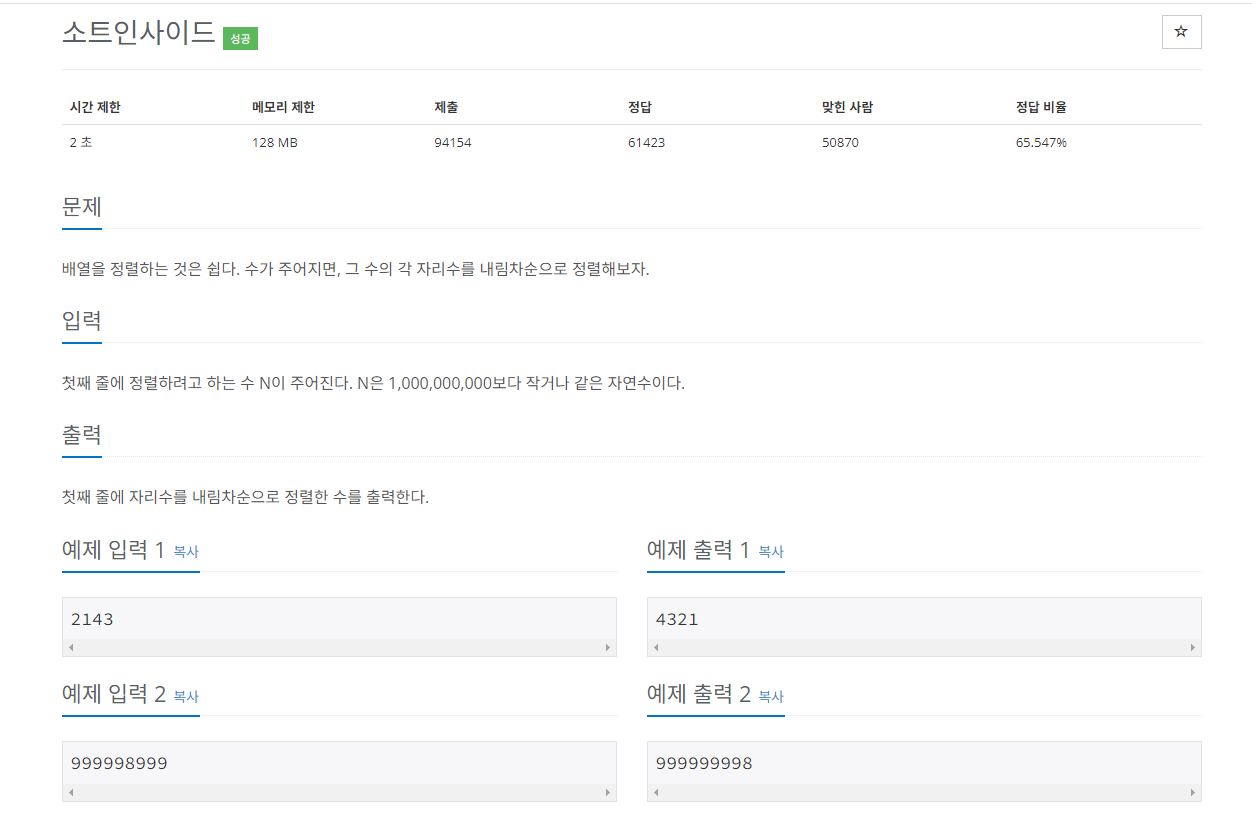
수 정렬하기 3

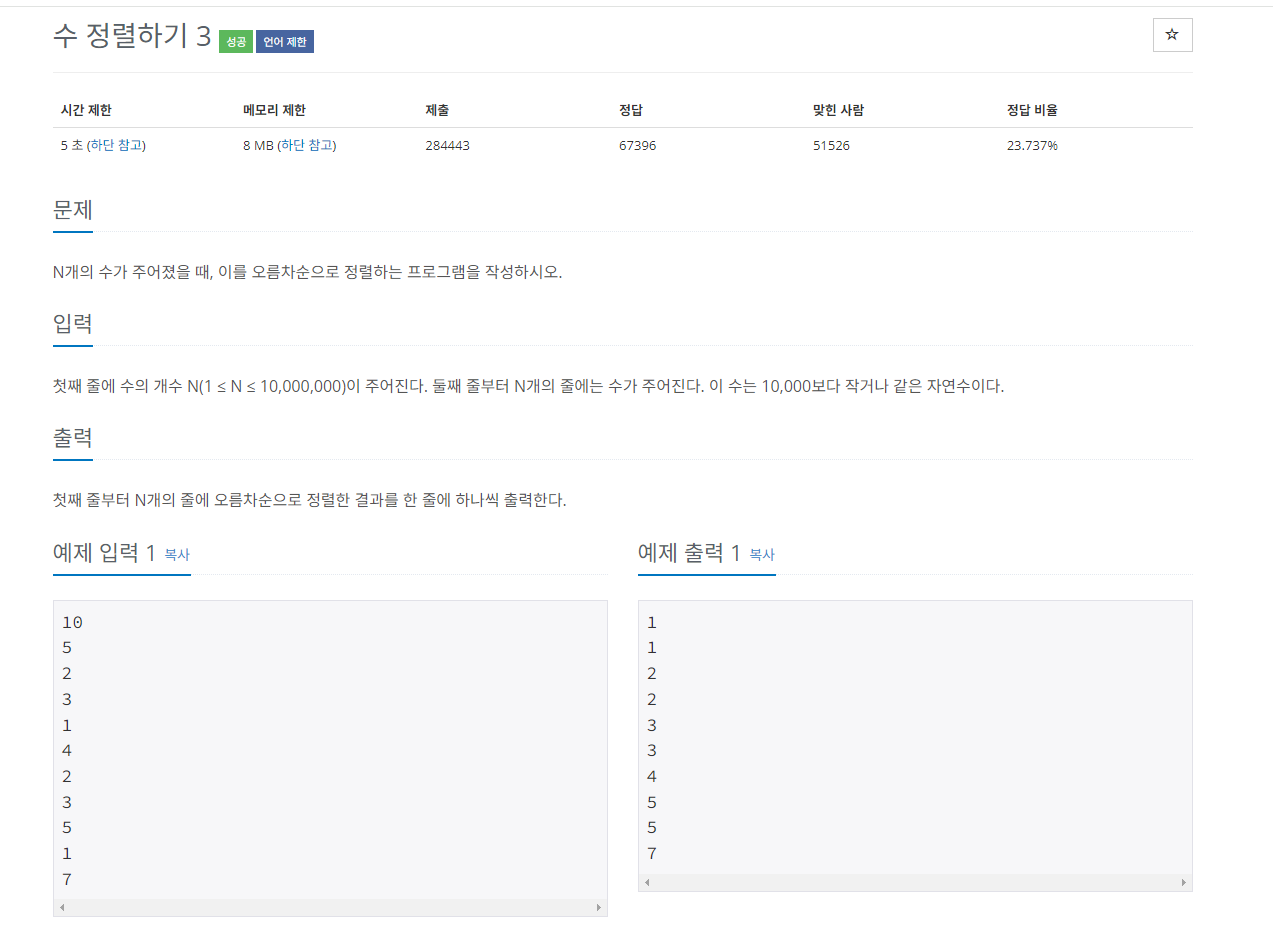
 이 문제는 n의 최대 10,000,000이 나올 수 있기 때문에 nlogn 보다 빠른 알고리즘이 필요하다. 숫자의 크기가 10,000 이하이기 때문에 기수 정렬과 함께 많이 사용되는 계수 정렬을 사용하여 문제를 풀어보려고  한다.

계수정렬은  수 값을 받아 수의 값을 인덱스 값으로 판단하고 그 인덱스에 해당하는 값을 1증가시키고 배열에 1이상인 것들을 출력시켜주면 된다. 

#include <iostream>
using namespace std;


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int n;
    cin >> n;
    int cnt[10001] = { 0 };
    int num = 0;

    for (int i = 1; i <= n; i++) {
        cin >> num;
        cnt[num]++;
    }
    for (int i = 0; i <= 10000; i++) {
        if (cnt[i] != 0) {
            for (int j = 0; j < cnt[i]; j++) {
                cout << i << "\n";
            }
        }
    }
}

오늘은 정렬에 대해 학습해보기로 했다.

정렬알고리즘의 종류에는 버블, 선택, 삽입, 퀵,병합,기수가 있다. 

1.버블정렬

버블정렬은 인접한 요소끼리 비교하고 swap연산을 통해 정렬을 한다. 

간단하게 구현가능하지만 시간복잡도는 O(n^2)으로 다른 정렬 알고리즘에 비해 느린편

문제 예시1.

버블정렬 프로그램1

문제에서 요구하는바는 swap이 끝나고 change가 false로 유지될때의 i 값이다. for문이 몇번이나 수행됐는지 구하면 된다.

n의 최대가 500,000이기 때문에 버블정렬은 사용할 수 없다. 

어떤 방법을 사용할지 생각해보자면 일단 버블정렬이 수행되는 방식에 대해 생각해보면 좋다.

버블정렬은 1~n-1까지 왼쪽에서 오른쪽으로 이동하면서 swap을 수행한다. 이는 swap할때 왼쪽으로 1칸씩만 이동할 수 있다는 것이다. 따라서 데이터 정렬하기전과 정렬 후의 index를 비교해서 가장 많이 이동한 값이 for문이 수행된 횟수가 나온다.  그리고 정렬이 끝난 후 마지막으로 for문이 돌때를 고려하여 max에 1을 더해준다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> Node;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	vector<pair<int, int>>a(n);

	for (int i = 0; i < n; i++) {
		cin >> a[i].first;
		a[i].second = i;
	}

	sort(a.begin(), a.end());
	int max = 0;

	for (int i = 0; i < n; i++) {
		if (max < a[i].second - i) {
			max = a[i].second - i;
		}
	}

	cout << max + 1;
}

2.선택 정렬

최대나 최소 데이터를 나열된 순으로 찾아가며 선택하고 그 수를 앞으로 보내면서 정렬하는 방법이다. 

문제예시2.

내림차순으로 자릿수 정렬하기

내장함수를 사용해도 풀 수 있지만 n의 길이가 길지 않아서 선택정렬을 통해 풀어보아도 된다.

#include <iostream>
#include <vector>
#include <string>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	string n;
	cin >> n;
	vector<int>a(n.size(), 0);

	for (int i = 0; i < n.size(); i++) {
		a[i] = stoi(n.substr(i,1));
	}

	for (int i = 0; i < n.size(); i++) {
		int max = i;
		for (int j = i + 1; j < n.size(); j++) {		//제일 큰 수  구하기
			if (a[j] > a[max]) {
				max = j;
			}
		}
		if (a[i] < a[max]) {
			int tmp = a[i];
			a[i] = a[max];
			a[max] = tmp;
		}
	}

	for (int i = 0; i < a.size(); i++) {
		cout << a[i];
	}
}

3.삽입정렬

삽입정렬은 현재 정렬된 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입하는 방식이다. 

문제예시3.

ATM인출 시간 계산하기

ATM에서 모든 사람이 가장 빠른 시간에 인출하려면 시간이 가장 적게 걸리는 사람이 먼저 인출할 수 있도록 그리디하게 접근하면 된다.

그럼 오름차순으로 정렬을 하면 되는데 n의 최댓값이 1,000이고 시간제한이 1초여서 O(n^2)이하인 정렬 알고리즘이면 모두 사용 가능하다. 지금은 삽입정렬을 사용해보려고 한다.

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	vector<int>a(n, 0);
	vector<int>s(n, 0);			//합배열

	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	for (int i=0; i < n; i++) {
		int insertval = a[i];
		int insertidx = i;
		for (int j = i - 1; j >= 0; j--) {            //i 왼쪽을 탐색
			if (a[i] > a[j]) {
				insertidx = j + 1;			//i가 j보다 크다면 i는 j보다 오른쪽에 있어야한다.
				break;
			}
			if (j == 0) {
				insertidx = 0;
			}
		}
		for (int j = i; j > insertidx; j--) {
			a[j] = a[j - 1];					//j~insertidx까지 값을 바꾸면서 insertidx의 값이 j로 가도록 한다.
		}
		a[insertidx] = insertval;
	}
	s[0] = a[0];

	for (int i = 1; i < n; i++) {
		s[i] = s[i - 1] + a[i];
	}
	int sum = 0;
	for (int i = 0; i < n; i++) {
		sum += s[i];
	}
	cout << sum;
}

스택

스택은 LIFO의 규칙, 즉 가장 나중에 들어온(최근에 들어온)값이 먼저 나가지는 자료구조로 보통 DFS나 백트레킹 문제에서 많이 사용된다.

큐

큐는 FIFO의 규칙, 즉 먼저 들어온(입력이 제일 먼저된)값이 먼저 나가지는 자료구조로 BFS에서 많이 사용된다.

문제 예1. 

오큰수

오큰수는 기준값을 기준으로 오른쪽에 있으면서  큰 수 중에서 가장 왼쪽에 있는 수를 뜻한다.

이 문제는 스택을 통해 풀 수 있는데 스택에 새로 들어오는 수가 top에 있는 수보다 크면 오큰수 배열에 저장한다. 

이때, 스택에는 수열의 값이 아닌 인덱스를 저장하여 pop되는 index에 오큰수를 저장한다. 

전체 배열을 순회하며 오큰수를 저장하고 정답배열을 순회하며 오큰수가 없는 칸에는 -1을 넣어준다. 

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	vector<int> a(n, 0);
	vector<int> answer(n, 0);
	
	stack<int> st;
	st.push(0);
    
    for(int i=0;i<n;i++){
        cin>>a[i];
    }

	for (int i = 1; i < n; i++) {
		while (!st.empty() && a[st.top()] < a[i]) {
			answer[st.top()] = a[i];
			st.pop();
		}
		st.push(i);
	}

	while (!st.empty()) {
		answer[st.top()] = -1;
		st.pop();
	}

	for (int i = 0; i < n; i++) {
		cout << answer[i] << " ";
	}

}

문제 예2.

절댓값 힙 구현하기

이 문제는 절댓값 힙을 구현하면 되는데  우선순위 큐를 사용하여 구현하면 된다. 우선 순위 큐는 큐와 달리 우선순위를 가진 값이 먼저 나가게 되는 자료구조이다. 

그리고 정렬기준을 따로 지정해줄 수 있는데 지정해준 기준대로 자동으로 정렬이 된다. 

이 문제에서는 정렬기준을 절댓값으로 두고 만약 절댓값이 같다면 음수를 우선 정렬해준다. 

#include <iostream>
#include <queue>
using namespace std;

struct compare
{
	bool operator()( int a, int b) {
		int first = abs(a);
		int second = abs(b);
		if (first == second) {
			return a > b;		//b가 우선순위
		}
		else {
			return first > second;		//second가 우선순위
		}
	}
};

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	priority_queue<int, vector<int>, compare> pq;
	
	int n;
	cin >> n;

	for (int i = 0; i < n; i++) {
		int rq;
		cin >> rq;

		if (rq == 0) {
			if (pq.empty()) {
				cout << "0\n";
			}
			else {
				cout << pq.top() << "\n";
				pq.pop();
			}
		}
		else {
			pq.push(rq);
		}
	}

}

투 포인터

투 포인터는 2개의 포인터로 문제를 푸는 것으로 즉, 가르키는 값을 2개로 둬서 문제를 푸는 방법이다. 

투 포인터는 2개의 값을 통해 나올 수 있는 경우의 수와 기준 값 즉 문제에서 요구하는 바에 따라 이동원칙을 만들고 이에 따라 코드로 구현하는 것이 핵심이다. 

예시 1. 좋은 수 구하기

이 문제는 수를 입력받아 배열을 만들고 정렬한 후 양쪽 끝에 투 포인터 i,j를 위치시키고 이동원칙을 만든 후 탐색을 수행하면 된다.

좋은 수를 K라고 했을 때 K이면 좋은 수이고 이것을 구하는 이동원칙을 구하면 된다. 

이동원칙(가정 i<j )

1. A[i]+A[j] >K  -> j-- 2. A[i]+A[j}<K i++ 3. A[i]+A[j] ==k count++ break; 

또한 정렬된 데이터에서 좋은 수를 만들 떄, 자기자신은 포함 시키면 안된다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	vector<int>A(N, 0);

	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	sort(A.begin(), A.end());
	int Result = 0;

	for (int k = 0; k < N; k++) {
		long find = A[k];
		int i = 0;
		int j = N - 1;
		while (i < j) {
			if (A[i] + A[j] == find) {
				if (i != k && j != k) {
					Result++;
					break;
				}
				else if (i == k) {
					i++;
				}
				else if (j == k) {
					j--;
				}
			}
			else if (A[i] + A[j] < find) {
				i++;
			}
			else {
				j--;
			}
		}

	}
	cout << Result << "\n";
}

※슬라이딩 윈도우

배열을 이동하면서 구한 부분 배열의 값을 업데이트 해주고 이에 따라 문제에서 주어진 조건을 확인하며 문제를 푸는 것이다. 

예시 문제 

최솟값찾기 1

이 문제에서는 부분 배열에서 최솟값을 구하는 것인데 최솟값을 구하는 범위가 i-L+1~ i 로 길이가 L인 부분 배열이다. 

이 때, n과 l의 최대 범위가 5,000,000이여서 O(nlogn)인 정렬을 사용할 수 가 없다. 그래서 이 문제에서는 슬라이딩 윈도우를 덱으로 구현하여 정렬효과를 볼 수 있다. 

deque<pair<int,int> mydeque; 라고 했을 때 숫자 값 , 인덱스 순서로 값을 넣어주고

현재값이 기존값보다 크다면 뒤에 넣어주고 만약 끝 인덱스- 주어진 부분배열 크기 했을 때, 처음 인덱스보다 크거나 같다면 처음값을 빼준다

현재값이 기존값보다 작다면 기존값을 삭제하고 넣어준다. 

이렇게 되면 덱에서 제일 첫번째에 있는 값이 부분배열의 최솟값이 된다.

#include <iostream>
#include <deque>
using namespace std;
typedef pair<int, int> Node;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, L;
	cin >> N>>L;
	deque<Node> dq;

	for (int i = 0; i < N; i++) {
		int now;
		cin >> now;

		while (dq.size() && dq.back().first > now) {
			dq.pop_back();
		}
		dq.push_back(Node(now, i));

		if (dq.front().second <= i - L) {
			dq.pop_front();
		}
		cout << dq.front().first << ' ';
	}
	
	
}

코딩테스트 공부를 하다가 난이도가 올라갈 수록 알고리즘을 분석하고 여러유형에 대해 이론적으로 이해하고 있는 부분이 부족하다고 생각이 들어 알고리즘과 여러 유형에 대해 익혀보는  시간을 가져보려고 한다. 

1. 구간 합

구한 합의 핵심이론은 a~b 구간 사이의 합을 구하는 것이다. 이 때, 배열을 두고 직접 합을 구할 때, 최악의 경우 i가 0이고 j가 N인 경우 시간복잡도가 O(N)이 나와서 연산 수가 많아지면 시간초과가 뜰 수 있다. 구간 합의 경우 연산 수 가 많아지는 경우가 많기 때문에 배열 합을 쓰는게 좋다. 

*합 배열 

합 배열은 기존의 배열에서 구간마다의 합을 만들어두는 것으로 이 배열을 만들어 두고 이를 활용하여 정답을 구한다면  

연산수가 O(1)로 줄어들게 된다. 

-1차원에서의 합 배열

1차원 배열에서 합 배열을 만들 때 S가 합배열이고 B가 배열이라고 했을 때, S[i]=S[i-1] + B[i] 이다. 

그리고 만약 i~j까지의 구간 합을 구한다면 S[j] -S[i] 로 정답을 구할 수 있다.

-2차원에서의 합 배열

2차원 배열에서 합 배열을 만들 때는 경우의 수를 2가지 생각해주어야 한다

일단 1행일때 열이 변하는경우, 1열일때, 행이 변하는 경우를 생각해보자면 1차원에서의 합 배열을 구하는 공식과 똑같은데 

1행 일때 -> S[i][j] = S[1][j-1]+B[i][j] 

1열 일때 -> S[i][j] = S[i-1][i]+ B[i][j]

-> 전까지의 합 + 현재위치의 값

나머지 행과 열 일때

S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+B[i][j] 

-> i-1 값(이전 값의 행)에서 열 방향에서의 합 + j-1(이전 값의 열)값에서 행 방향  + 중복되게 더해진 값 - 현재 위치의 값

그리고 X1,Y1 ~ X2,Y2 까지의 구간 합을 구한다면

S[X2][Y2]-S[X1-1][Y2]-S[X2][Y1-1]+S[X1][Y1]

->X2,Y2까지의 구간합 - X1-1 값에서의 열 방향에서의 합 - Y1-1 값에서의 행 방향에서의 합 + 중복되게 빼진 값

예시 문제

나머지 합 구하기

이 문제에서 보면 N의 최대값이 10^6으로 최악의 경우 1초안에 연산하기는 힘들기 때문에 합 배열을 사용해야한다. 

※핵심 아이디어

1. (A+B) % C = ((A%C)+(B%C))%C -> 특정 구간 수를 나머지 연산해서 더한 값을 나머지 연산하는 것이나 구간합을 나머지 연산한 값이나 같다. 

2. if S[j]%M == S[i]%M 이라면 (S[j]-S[i])%M==0이다. 

흐름을 살펴보자면 

1. 합 배열을 만든다.

2. %M의 값으로 배열을 업데이트 해준다.

3. 경우의 수를 세어준다. (0일때는 0인 개수만큼 경우의 수를 추가, 2보다 클때에는 조합을 통해 경우의 수를 추가)

#include <iostream>
#include <vector>
using namespace std;

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, M;
	cin >> N >> M;
	vector<long> S(N, 0);
	vector<long> C(N, 0);
	long answer = 0;
	cin >> S[0];

	for (int i = 1; i < N; i++) {
		int tmp = 0;
		cin >> tmp;
		S[i] = S[i - 1] + tmp;
	}
	for (int i = 0; i < N; i++) {
		int r = S[i] % M;
		if (r == 0) {
			answer++;
		}
		C[r]++;
	}
	for (int i = 0; i < M; i++) {
		if (C[i] > 1) {
			answer += (C[i] * (C[i] - 1) / 2);
		}
	}

	cout << answer << "\n";
}

무게에 따른 사람의 수를 모두 저장해준다음 그 벡터를 순회하면서

같은 무게가 있으면 어디에 앉든 균형을 이루기 때문에 조합으로 수를 구해주고

2 3 4 m 자리가 있어서 나올 수 있는 비율은 2:3 2:4=1:2 3:4 가 있기 때문에

이 에 맞는 값이 있다면 경우의 수 를 추가해주면 된다.

#include <string>
#include <vector>

using namespace std;

long long solution(vector<int> weights) {
    long long answer = 0;
    vector<long long> cnt(1001, 0);      //몸무게 별 사람수
    for (int i = 0; i < weights.size(); i++) {
        cnt[weights[i]]++;
    }
    //나올수 있는 비율 2:3 2:4=1:2 3:4
    for (int i = 0; i < weights.size(); i++) {
        if (weights[i] % 2 == 0) {                //2:3
            long long base = (weights[i] / 2) * 3;
            if (base <= 1000) answer += cnt[base];
        }
        if (weights[i] % 3 == 0) {                //3:4
            long long base = (weights[i] / 3) * 4;
            if (base <= 1000) answer += cnt[base];
        }
        long long base = weights[i] * 2;
        if (base <= 1000) answer += cnt[base];
    }

    for (int i = 100; i <= 1000; i++) {
        if (cnt[i] >= 2)
            answer += (long long)(cnt[i] * (cnt[i] - 1)) / 2;           //같을 때
    }

    return answer;
}

ext의 값이 val_ext보다 낮은 것을 저장하고 sort_by값에 따라 오름차순 정렬하는 문제이다. 처음에는 switch 문을 통해 idx1, idx2를 정해서 저장 및 정렬을 하려고 했는데 switch 문에는 문자열을 그냥 쓸 수 가 없는 것 같아서 map 자료형을 통해 idx 값을 정해서 저장 및 분류를  해주었다. 또한 compare 함수로 기준 값에 따라 오름차순 정렬되도록 만들었다.

코드

#include <string>
#include <vector>
#include <algorithm>
#include <map>

using namespace std;
map<string,int> m1={{"code",0},{"date",1},{"maximum",2},{"remain",3}};
int idx;
bool compare(const vector<int> &data1,const vector<int> &data2){
    return data1[idx]<data2[idx];
}
vector<vector<int>> solution(vector<vector<int>> data, string ext, int val_ext, string sort_by) {
    vector<vector<int>> answer;
    idx=m1[sort_by];
    for(auto d: data){
        if(d[m1[ext]]<=val_ext){
            answer.push_back(d);
        }
    }
    sort(answer.begin(),answer.end(),compare);
    return answer;
}

1. 입력액션 지정

특정 키를 눌렀을 때, 해당 행동을 하게 하기 위해서는 일단 키를 눌렀을 때 작동하게 할 캐릭터의 Input/Actions 폴더에 들어가서 우클릭 후 입력 / 입력액션을 클릭하고 원하는 이름으로 지정해주면 된다.

만든 후 기본 설정으로 두면 된다. 

2. 매핑 컨텍스트에 키 추가

Input 폴더의 입력 매핑 컨텍스트를 더블클릭하여 들어간 뒤 +키를 눌러 매핑을 추가해주고 키 값은 키보드 버튼을 누른뒤 원하는 키를 입력하면 된다.

3. 움크리기 애니메이션 추가

애니메이션에 움크리는 애니메이션을 추가해서 동작할 수 있도록한다.

4. 동작 블루 프린터 추가

키를 추가해주었다면 키를 통해 작동할 캐릭터의 블루프린터로 들어 간 후, 이벤트 그래프에서 커스텀 이벤트를 추가해서 동작하도록 만들어 주면 된다. 

5. 함수 내부 동작

함수는  커스텀이벤트를 추가해서 구현해두었는데 이 때 전에 추가해둔 IA_Crouch 를 불러온다음 키가 눌릴떄, 즉 Started에서 만약 달리는 중과 움크리는 중이 아니라면 움크린 불린값을 True로 만들어준다. 이때, 애니메이션 그래프에서 Crouched Locomotion으로 애니메이션이 넘어가지게 된다. 그 이후 걷는 속도를 낮춰주고 카메라의 거리를 조금 멀리로 바꿔주는데 이때, 400 -> 500의 값을 Lerp하게 즉, 스무스하게 넘어가도록 해준다.

의사코드가 잘나와있는 문제라 그대로 구현만 해주면 쉽게 풀리는 문제이다. 중요한 건 위 아래 왼쪽 오른쪽을 탐색하고 그 탐색한 값이 표의 크기 안에서 존재하는 지 확인해주면 된다.

#include <string>
#include <vector>

using namespace std;

int dh[4]= {0,1,-1,0};
int dw[4]= {1,0,0,-1};
int solution(vector<vector<string>> board, int h, int w) {
    int answer = 0;
    int size=board.size();
    int wsize=board[1].size();
    for(int i=0;i<4;i++){
        int h_check=h+dh[i];
        int w_check=w+dw[i];
        if(h_check>=0&&h_check<size&&w_check>=0&&w_check<wsize){
            if(board[h][w]==board[h_check][w_check]){
                answer++;
            }
        }
    }
    return answer;
}

참가자 이름과 완주자이름을 비교하여 완주하지못한 사람을 찾으면 된다. 

나는 map 자료형을 사용해서 참여자 벡터를 순회하면서 해당 이름의 값을 증가시켜주고 그 뒤에 완주자 벡터를 순회하면서 해당 이름의 값을 줄여준다. 이때 해당 이름의 값이 1보다 크거나 같을 경우 통과하지 못하였다는 것이므로 answer에 추가해준다. 

동명이인이 있을 수 도 있어서 answer에 넣은 뒤 해당 이름의 값을 줄여준다. 

#include <string>
#include <vector>
#include <map>
using namespace std;
map<string,int> m1;
string solution(vector<string> participant, vector<string> completion) {
    string answer = "";
    for(int i=0;i<participant.size();i++){
        m1[participant[i]]++;
    }
    for(int i=0;i<completion.size();i++){
        m1[completion[i]]--;
    }
    for(int i=0;i<participant.size();i++){
        if(m1[participant[i]]>=1){
            answer+=participant[i];
            m1[participant[i]]--;
        }
    }
    return answer;
}